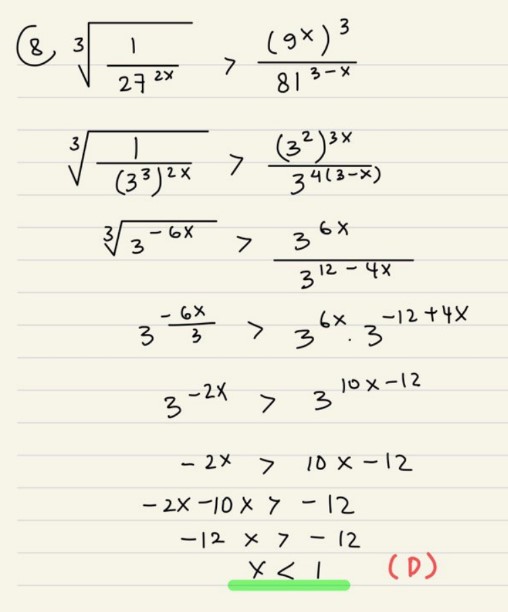Soal dan Pembahasan Logaritma Kelas X Sukino Peminatan LKS 5 Bag A no 16

16. Himpunan penyelesaian dari persamaan logaritma ³log ³log (3^{x + 1}- 2) - ³log x = 1 adalah ...

a. {1}

b. {³log 2}

c. {}

d. {0}

e. {-1}

Jawaban : C

³log ³log (3^{x + 1}- 2) - ³log x = 1

³log (³log ((3^{x + 1}- 2) / x)) = ³log 3

³log (3^{x + 1}- 2) / x = 3

³log (3^{x + 1}- 2) = 3x

³log (3^{x + 1}- 2) = ³log 3^3x

3^{x + 1}- 2 = 3^3x

3^{x + 1}- 2 = (3^x)³

misalkan a = 3^x 

3 . 3^x - 2 = (3^x)³

3a - 2 = a³

0 = a³ - 3a + 2

cari faktornya (ada beberapa grouping)

0 = a³ - 3a + 2

0 = a³ + 2a² - 2a² - 4a + a + 2

0 = a² (a + 2) - 2a(a + 2) + (a + 2)

0 = (a + 2) (a²- 2a + 1)

0 = (a + 2)(a - 1)(a - 1)

sehingga,

a = - 2

3^x = - 2 (x tidak terdefinisi, karena tidak ada pangkat dari 3 yang menghasilkan nilai minus)

a = 1

3^x = 1

x = ³log 1

x = 0

namun pada soal perlu di cek lagi,

³log x, x harus > 0

maka HP :{}

Soal dan Pembahasan Logaritma Kelas X Sukino Peminatan LKS 5 Bag A no 15

15. Jika a dan b adalah akar-akar persamaan 5^{5log (4x2 + 3)} + 4^{2log (x2 - 1)} - 39 = 0 , maka a + b = ...

a. 5

b. √7 + √5

c. 2

d. 0

e. - 2

Jawaban : D

5^{5log (4x2 + 3)} + 4^{2log (x2 - 1)} - 39 = 0 

5^{5log (4x2 + 3)} + 2^{22log (x2 - 1)} - 39 = 0 

4x² + 3 + 2^{2log (x2 - 1)2}- 39 = 0

4x² + 3 + 2^{2log (x2 - 1)2}- 39 = 0

4x² + 3 + (x²- 1)² - 39 = 0

4x² + 3 + x⁴- 2x² + 1 - 39 = 0

x⁴ + 2x² - 35 = 0

(x² - 5) (x² + 7) = 0

maka

x² = 5

x = ±√5

x² = - 7

x = √(-7)  ~ tidak rasional

maka x1 = √5 dan x2 = - √5

a + b = x1 + x2 = √5 - √5 = 0

Soal dan Pembahasan Logaritma Kelas X Sukino Peminatan LKS 5 Bag A no 14

14. Jika x1 dan x2 adalah akar-akar persamaan logaritma (5 - log x²) . log x = 3, maka x1² + x2² = ...

a. 0

b. 10¹

c. 10²

d. 10³

e. 10³ + 10²

Jawaban : E

(5 - log x²) . log x = 3

(5 - 2 log x) . log x = 3

misalkan log x = a

(5 - 2a) . a = 3

5a - 2a² = 3

0 = 2a² - 5a + 3

0 = (2a - 3)(a - 1)

maka x1 :

2a = 3

a = 3/2

kembalikan ke nilai x

log x = 3/2

x = 10^3/2

untuk x2 :

a = 1

log x = 1

x = 10¹

x = 10

yang ditanyakan :

x1² + x2²

= (10^3/2)² + (10)²

= 10³ + 10²

Soal dan Pembahasan Logaritma Kelas X Sukino Peminatan LKS 5 Bag A no 13

 13. Jika x1 dan x2 dengan x1 > x2 merupakan akar-akar persamaan logaritma :

(x - a) / (x -a)^{log (x - a)} =1

dengan a konstanta positif, maka nilai dari ekspresi (x1 - x2) adalah ...

a. 6

b. 7

c. 8

d. 9

e.10

Jawaban : D

(x - a) / (x -a)^{log (x - a)} =1

(x - a) = (x -a)^{log (x - a)}

beri log di kedua ruas

log (x - a) = log (x -a)^{log (x - a)}

log (x - a) = log (x -a) .  log (x -a)

log (x - a) = log² (x -a)

0 = log² (x -a) - log (x - a)

0 = log (x - a) (log (x - a) - 1)

maka x1 :

log (x - a) - 1 = 0

¹⁰log (x - a) = 1

x - a = 10¹

x = 10 + a

sedangkan x2 :

log (x - a) = 0

¹⁰log (x - a) = 0

x - a = 10⁰

x = 1 + a

x1 > x2 dengan a konstanta positif,

x1 - x2

= 10 + a - (1 + a)

= 10 + a - 1 - a

= 9

Soal dan Pembahasan Logaritma Kelas X Sukino Peminatan LKS 5 Bag A no 12

12. Jika a > 1, maka penyelesaian dari persamaan [^alog(2x + 1)][³log √a] = 1 adalah ...

a. 1

b. 2

c. 3

d. 4

e. 5

Jawaban : D

[^alog(2x + 1)][³log √a] = 1

[^alog(2x + 1)][³log a^1/2] = 1

[^alog(2x + 1)][1/2 ³log a] = 1

1/2 . ³log a . ^alog(2x + 1) = 1

1/2 . ³log (2x + 1) = 1

³log (2x + 1) = 2

³log (2x + 1) = ³log 3²

2x + 1 = 3²

2x + 1 = 9

2x = 8

x = 4

Soal dan Pembahasan Logaritma Kelas X Sukino Peminatan LKS 5 Bag A no 11

11. Jumlah semua nilai x yang memenuhi persamaan logaritma ²log²(4x - 4) - ²log(4x - 4)⁴= - 3 adalah ...

a. 3 2/5

b. 4

c. 4 1/2

d. 5

e. 9

Jawaban : C

²log²(4x - 4) - ²log(4x - 4)⁴= - 3

²log²(4x - 4) - 4 . ²log(4x - 4) = - 3

misalkan :

²log(4x - 4) = a

maka,

a² - 4a = -3

a² - 4a + 3 = 0

(a - 3)(a - 1) = 0

a = 3 atau a = 1

kembalikan lagi dalam bentuk x,

²log(4x - 4) = a

untuk a = 3

²log(4x - 4) = 3

2³ = 4x - 4

8 = 4x - 4

4x = 8 + 4

4x = 12

x = 3

 untuk a = 1

²log(4x - 4) = 1

2¹ = 4x - 4

4x = 2 + 4

4x = 6

x = 6/4

x = 3/2

jumlah x1 dan x2 :

3 + 3/2

= 6/2 + 3/2

= 9/2

= 4 1/2

Soal dan Pembahasan Logaritma Kelas X Sukino Peminatan LKS 5 Bag A no 10

10. Himpunan penyelesaian dari eprsamaan logaritma :

^xlog (10x³ - 9x) = ^xlog x⁵

adalah ...

a. {3}

b. {1,3}

c. {0,1,3}

d. {-3,-1,1,3}

e. {-3,-1,0,1,3}

Jawaban : A

^xlog (10x³ - 9x) = ^xlog x⁵

10x³ - 9x = x⁵

0 = x⁵ - 10x³ + 9x

0 = x (x⁴ - 10x² + 9)

0 = x (x² - 1)(x² - 9)

x = 0

x² - 1 = 0

x² = 1

x = -1 atau x = 1

x² - 9 = 0

x² = 9

x = - 3 atau x = 3

cek lagi, 

^xlog (10x³ - 9x) = ^xlog x⁵

basis = x

g(x) = 10x³ - 9x

h(x) = x⁵

basisnya (x) harus ≠ 1 dan > 0, g(x) > 0, h(x) > 0

untuk x = 0, tidak memenuhi : basis > 0

untuk x = - 1, tidak memenuhi : basis > 0

untuk x = 1, tidak memenuhi : basis ≠ 1

untuk x = - 3, tidak memuhi : basis > 0

untuk x = 3, memenuhi

jadi HP : x = 3

Soal dan Pembahasan Logaritma Kelas X Sukino Peminatan LKS 5 Bag A no 9

9. Persamaan logaritma ²log² x - 3 . ²log x - 10 = 0 mempunyai solusi x1 dan x2. Nilai x1 . x2 = ...

a. 2^-5

b. 2^-3

c. 2²

d. 2³

e. 2⁵

Jawaban : D

²log² x - 3 . ²log x - 10 = 0

A = 1

B = - 3

C = - 10

a = 2

x1 . x2 = a^-B/A

x1 . x2 = 2^-(-3)/1

x1 . x2 = 2³

Soal dan Pembahasan Logaritma Kelas X Sukino Peminatan LKS 5 Bag A no 8

8. Jika ^√(2√2)log x = 1/(1 - log 5) , maka x = ...

a. 10

b. 100

c. 1000

d. 0,1

e. ⁴√1000

Jawaban : E

^√(2√2)log x = 1/(1 - log 5)

^{2^3/4}log x = 1/(log 10 - log 5)

4/3 . ²log x = 1/(log 10/5)

4/3 . ²log x = 1/(log 2)

4/3 . ²log x . log 2 = 1

4/3 . log 2 . ²log x = 1

4/3 . log x = 1

log x = 3/4

¹⁰log x = 3/4

10^3/4 = x

x = ⁴√1000

Soal dan Pembahasan Logaritma Kelas X Sukino Peminatan LKS 5 Bag A no 7

7. Jika ^axlog b = z, maka ^bylog a = ... 

a. x . y . z

b. y/xz

c. xz/y

d. 1/xyz

e. z/xy

Jawaban : D

^axlog b = z

1/x . ^alog b = z

^alog b = xz

b = a^xz

maka,

^bylog a

= ^(axz)ylog a

= ^axzylog a

= 1/xyz . ^alog a

= 1/xyz

Soal dan Pembahasan Logaritma Kelas X Sukino Peminatan LKS 5 Bag A no 6

6. Penyelesaian persamaan ⁹log x - ^xlog 3 = 1/2 adalah x1 dan x2. Nilai x1 . x2 = ...

a. - 81

b. - 9

c. 1/3

d. 3

e. 9

Jawaban : D

 ⁹log x - ^xlog 3 = 1/2

 ³²log x - ^xlog 3 = 1/2

 1/2 . ³log x - 1 / ³log x = 1/2

kalikan dengan ³log x agar penyebutnya hilang

1/2 ³log² x - 1 = 1/2 ³log x

1/2 ³log² x - 1/2 ³log x - 1 = 0

A = 1/2

B = - 1/2

C = -1

a = 3

perkalian dari nilai x1.x2 :

x1.x2 = a^-B/A

x1.x2 = 3^{-(-1/2)/(1/2)}

x1. x2 = 3

ALTERNATIF PENYELESAIAN LAIN

 ⁹log x - ^xlog 3 = 1/2

 ³²log x - ^xlog 3 = 1/2

 1/2 . ³log x - 1 / ³log x = 1/2

misalkan a = ³log x

1/2 a - 1/a = 1/2

dikalikan dengan a agar penyebutnya hilang

1/2 a² - 1 - 1/2a = 0

dikalikan dengan 2 agar penyebutnya hilang

a² - 2 - a = 0

a² - a - 2 = 0

(a - 2)(a + 1) = 0

a = 2

atau a = -1

jika a = 2

maka 

a = ³log x

2 = ³log x

3² = x

x = 9

jika a = - 1

maka

a = ³log x

-1 = ³log x

3^-1 = x

x = 1/3

hasil kali x1. x2

= 9 . 1/3

= 3

Soal dan Pembahasan Logaritma Kelas X Sukino Peminatan LKS 5 Bag A no 5

5. Jika

6^{3x - y - 1} / 2^{3x - y} = 9/2, maka ^{3x - y}log √(3√3) = ...

a. 1/4

b. 1/3

c. 1/2

d. 2/3

e. 3/4

Jawaban : E

6^{3x - y - 1} / 2^{3x - y} = 9/2

6^{3x - y} . 6^-1/ 2^{3x - y} = 9/2

1/6 . (6/2)^{3x - y}= 9/2

1/6 . 3^{3x - y}= 9/2

3^{3x - y}/6 =  9/2

kalikan ruas kanan dengan 3/3 agar penyebutnya menjadi 6, sama dengan ruas kiri

3^{3x - y}/6 = 27/6

3^{3x - y} = 27

3^{3x - y} = 3³

3x - y = 3

maka,

^{3x - y}log √(3√3)

= ³log √(3 . 3^1/2)

= ³log √(3^3/2)

= ³log 3^3/4

= 3/4 ³log 3

= 3/4

Soal dan Pembahasan Logaritma Kelas X Sukino Peminatan LKS 5 Bag A no 4

 4. Nilai x yang memenuhi persamaan

^xlog 2 / (²log x - 4) = - 1/3

adalah ...

a. 1 atau 4

b. 1 atau 8

c. 2 atau 4

d. 2 atau 8

e. 4 atau 8

Jawaban : D

^xlog 2 / (²log x - 4) = - 1/3

3 . ^xlog 2 = - (²log x - 4)

3 . ^xlog 2 = 4 - ²log x

misalkan 

²log x = a

maka,

^xlog 2 = 1/a

sehingga,

3 . ^xlog 2 = 4 - ²log x

3 . 1/a = 4 - a

dikalikan dengan a untuk menghilangkan penyebut,

3 = 4a - a²

a² - 4a + 3 = 0

(a - 3)(a - 1) = 0

a = 3 atau a = 1 

jika a = 3, maka

²log x = 3

2³ = x

x = 8

jika a = 1, maka

²log x = 1

2¹ = x

x = 2

nilai x yang memenuhi :

2 atau 8

Soal dan Pembahasan Logaritma Kelas X Sukino Peminatan LKS 5 Bag A no 3

3. Nilai x yang memenuhi persamaan :

³log (4/9 - 3^x) = x - 1

adalah ...

a. - 1/3

b. - 1/2

c. - 1

d. - 2

e. - 3

Jawaban : D

³log (4/9 - 3^x) = x - 1

³log (4/9 - 3^x) = ³log 3^{x - 1}

4/9 - 3^x = 3^{x - 1}

4/9 - 3^x = 3^x . 3^-1

4/9 - 3^x = 3^x . 1/3

dikalikan dengan 9 agar penyebutnya hilang

4 - 9 . 3^x = 9 . 3^x . 3

4 - 9. 3^x = 27. 3^x

4 = 27. 3^x + 9 . 3^x

4 = 36 . 3^x

4/36 = 3^x

1/9 = 3^x

3^-2 = 3^x

x = - 2

Soal dan Pembahasan Logaritma Kelas X Sukino Peminatan LKS 5 Bag A no 2

 2. Nilai x yang memenuhi persamaan :

3^{2log x} = 2 .  3^{2log x} - 9

adalah ...

a. 1/4

b. 1/2

c. 2

d. 3

e. 4

Jawaban : E

3^{2log x} = 2 .  3^{2log x} - 9

misalkan a = 3^{2log x}

a = 2a - 9

9 = 2a - a

a = 9

kembalikan lagi dalam bentuk x

3^{2log x} = 9

²log x = ³log 9 

²log x = ³log 3²

²log x = 2

x = 2²

x = 4

 

Soal dan Pembahasan Logaritma Kelas X Sukino Peminatan LKS 5 Bag A no 1

1. Hasil kali akar-akar persamaan :

²log (x² - x + 1) = ⁵log (x² - x + 1)

adalah ...

a. 1/4

b. 1/2

c. 2

d. 3

e. 4

Jawaban :

²log (x² - x + 1) = ⁵log (x² - x + 1)

x² - x + 1 = 1 (karena ²log 1 = ⁵log 1 = 0)

x² - x + 1 - 1 = 0

x² - x = 0

a = 1

b = - 1

c = 0

hasil kali akar-akar persamaan :

x1 . x2 = c/a

x1 . x2 = 0/1

x1 . x2 = 0

*tidak ada di dalam pilihan jawaban*

Kunci Jawaban Matematika Sukino Kelas X Peminatan Bab 2 LKS 4 no 6

Carilah HP untuk setiap persamaan logaritma berikut.

6. 

^{x + 3}log (x + 2) = ^{x + 3}log (3x - 2)

Jawaban :

x + 2 = 3x - 2

2 + 2 = 3x - x

4 = 2x

x = 4/2

x = 2

cek dulu,

x + 3

= 2 + 3

= 5 > 0

maka HP : x = 2

Kunci Jawaban Matematika Sukino Kelas X Peminatan Bab 2 LKS 4 no 5

Carilah HP untuk setiap persamaan logaritma berikut.

5.

⁴log (2x² + 3x - 1) = ⁷log (2x² + 3x - 1)

Jawaban :

⁴log (2x² + 3x - 1) = ⁷log (2x² + 3x - 1)

2x² + 3x - 1 = 1 (karena ⁴log 1 = ⁷log 1 = 0)

2x² + 3x - 1 - 1 = 0

2x² + 3x - 2 = 0

(2x - 1)(x + 2) = 0

2x = 1

x = 1/2

atau

x = - 2 

Kunci Jawaban Matematika Sukino Kelas X Peminatan Bab 2 LKS 4 no 4

Carilah HP untuk setiap persamaan logaritma berikut.

4.

²log (x² - 2x + 1) = ²log (2x² - 2)

Jawaban :

²log (x² - 2x + 1) = ²log (2x² - 2)

x² - 2x + 1 = 2x² - 2

0 = 2x² - x² + 2x - 2 - 1

0 = x² + 2x - 3

0 = (x + 3) (x - 1)

x = - 3

atau x = 1

cek dulu

jika x = - 3,

x² - 2x + 1 > 0

(-3)² - 2(-3) + 1 > 0

9 + 6 + 1 > 0

16 > 0

sedangkan untuk

2x² - 2 > 0

2(-3)² - 2 > 0

18 - 2 > 0

16 > 0

maka x = - 3 termasuk HP

jika x = 1

x² - 2x + 1 > 0

(1)² - 2(1) + 1 > 0

1 - 2 + 1 > 0

0 ≯ 0

tidak lebih besar dari 0, maka x = 1 bukan termasuk HP (karena sudah tidak memenuhi, maka tidak perlu di cek untuk 2x² - 2)

maka HP : x = - 3 

Kunci Jawaban Matematika Sukino Kelas X Peminatan Bab 2 LKS 4 no 3

Carilah HP untuk setiap persamaan logaritma berikut.

3.

³log (4x - 15) = ⁷log (4x - 15)

Jawaban :

³log (4x - 15) = ⁷log (4x - 15)

4x - 15 = 1 (karena ³log 1 = ⁷log 1 = 0)

4x = 16

x = 4

HP : x = 4

Kunci Jawaban Matematika Sukino Kelas X Peminatan Bab 2 LKS 4 no 2

Carilah HP untuk setiap persamaan logaritma berikut.

2.

^{2x + 3}log (x² - 3x + 2) = ^{2x + 3}log (5x - 10)

Jawaban :

^{2x + 3}log (x² - 3x + 2) = ^{2x + 3}log (5x - 10)

x² - 3x + 2 = 5x - 10

x² - 3x - 5x+ 2 + 10 = 0

x² - 8x + 12 = 0

(x - 6)(x - 2) = 0

x = 6

atau

x = 2

cek dulu,

jika x = 6

2x + 3 

= 2 .6  + 3

= 12 + 3

= 15 > 0

maka x = 6 termasuk HP

jika x = 2

2x + 3

= 2 . 2 + 3

= 4 + 3

= 7 > 0

maka x = 2 juga termasuk HP

HP : x = 2 dan x = 6

Kunci Jawaban Matematika Sukino Kelas X Peminatan Bab 2 LKS 4 no 1

Carilah HP untuk setiap persamaan logaritma berikut.

1.

^{x - 1}log (5x² - 4x) = ^{x - 1}log (x² + 8)

Jawaban :

^{x - 1}log (5x² - 4x) = ^{x - 1}log (x² + 8)

5x² - 4x = x² + 8

5x² - x² - 4x - 8 = 0

4x² - 4x - 8 = 0

dibagi 4 agar lebih sederhana :;

x² - x - 2 = 0

(x - 2)(x + 1) = 0

x = 2

atau x = - 1

cek dulu,

bila x = 2, 

x - 1 

= 2 - 1

= 1 > 0

karena > 0 maka termasuk ke dalam HP

bila x = -1

x - 1

= -1 - 1

= -2

karena tidak lebih besar dari 0, maka x = -1 tidak termasuk ke dalam HP

HP : x = 2

Kunci Jawaban Matematika Sukino Kelas X Peminatan Bab 2 LKS 3 Bagian B no 3d

3. Selesaikan sistem persamaan berikut. 

d.  

²log (4 + x - 5y) = 0

²log (x + 1) = 1 + 2 ²log y 

Jawaban :

²log (4 + x - 5y) = 0

²log (4 + x - 5y) = ²log 1

4 + x - 5y = 1

x - 5y = - 3 ... (i)

x = - 3 + 5y

²log (x + 1) = 1 + 2 ²log y

²log (x + 1) = ²log 2 + ²log y²

²log (x + 1) = ²log 2y²

x + 1 = 2y²

- 3 + 5y + 1 = 2y²

5y - 2 = 2y²

0 = 2y² - 5y + 2

0 = (2y - 1)(y - 2)

maka

2y - 1 = 0

2y = 1

y = 1/2

atau 

y - 2 = 0

y = 2

jika y = 1/2

maka 

x = - 3 + 5y

x = - 3 + 5 . 1/2

x = - 3 + 5/2

x =  - 1/2

jika y = 2

maka

x = - 3 + 5y

x = - 3 + 5 . 2

x = - 3 + 10

x = 7

Kunci Jawaban Matematika Sukino Kelas X Peminatan Bab 2 LKS 3 Bagian B no 3c

 3. Selesaikan sistem persamaan berikut. 

c.

⁵log (3x - y) + ⁵log 6 = ⁵log 24

7^5x : 7^3y  = 1

Jawaban :

⁵log ((3x - y). 6) = ⁵log 24

6 (3x - y) = 24

3x - y = 4 ... (i)

7^5x : 7^3y  = 1

7^{5x - 3y}  = 7⁰

5x - 3y = 0 ... (ii)

lakukan eliminasi (i) dan (ii) dengan mengkalikan (i) x 3

9x - 3y = 12

5x - 3y = 0

--------------- -

4x = 12

x = 3

masukkan nilai x ke dalam persamaan (i)

3x - y = 4

3 . 3 - y = 4

9 - y = 4

- y = - 5

y = 5

Kunci Jawaban Matematika Sukino Kelas X Peminatan Bab 2 LKS 3 Bagian B no 3b

3. Selesaikan sistem persamaan berikut. 

b.

2x : 4y = 8

³log x - ³log 5 = ³log (y + 1) + ³log 2

Jawaban :

2x : 4y = 8

2x = 32y

x = 16y ... (i)

³log x - ³log 5 = ³log (y + 1) + ³log 2

³log x/5 = ³log (y + 1) . 2

x/5 = 2y + 2

x = 5(2y + 2)

x = 10y + 10 ... (ii)

masukkan persamaan (i) ke dalam persamaan (ii)

x = 10y + 10

16y = 10y + 10

6y = 10

y = 10/6

y = 5/3

masukkan nilai y ke dalam persamaan (i)

x = 16y

x = 16 . 5/3

x = 80/3

x = 26 2/3

Kunci Jawaban Matematika Sukino Kelas X Peminatan Bab 2 LKS 3 Bagian B no 3a

3. Selesaikan sistem persamaan berikut. 

a.

²log 7 = 1 + ²log (p - 3q) 

3p = 18 + 4q

Jawaban :

²log 7 = 1 + ²log (p - 3q) 

²log 7 = ²log 2 + ²log (p - 3q) 

²log 7 = ²log 2(p - 3q) 

²log 7 = ²log (2p - 6q) 

7 = 2p - 6q ... (i)

3p = 18 + 4q

3p - 4q = 18 

18 = 3p - 4q ... (ii)

lakukan eliminasi (i) dan (ii) dengan (i) x 3 dan (ii) x 2

21 = 6p - 18q

36 = 6p - 8q

---------------- -

- 15 = - 10q

q = 15/10

q = 3/2

masukkan nilai q ke dalam persamaan (i)

7 = 2p - 6q

7 = 2p - 6 . 3/2

7 = 2p - 9

16 = 2p

p = 8

Kunci Jawaban Matematika Sukino Kelas X Peminatan Bab 2 LKS 3 Bagian B no 2g

 2. Selesaikan

g.

²log (2x + 5) - 2 ²log 2x = 2

²log (2x + 5) - ²log (2x)² = ²log 2²

²log (2x + 5) - ²log 4x² = ²log 4

²log ((2x + 5) / 4x²)= ²log 4

(2x + 5) / 4x² = 4

2x + 5 = 16x²

0 = 16x² - 2x - 5

0 = (2x + 1)(8x - 5)

2x + 1 = 0

2x = - 1

x = - 1/2

8x - 5 = 0

8x = 5

x = 5/8

Kunci Jawaban Matematika Sukino Kelas X Peminatan Bab 2 LKS 3 Bagian B no 2f

2. Selesaikan

f. 

²log 4x - 2 ²log 5 = 3

²log 4x - ²log 5² = ²log 2³

²log (4x / 25) = ²log 8

4x / 25 = 8

4x = 200

x = 50

Kunci Jawaban Matematika Sukino Kelas X Peminatan Bab 2 LKS 3 Bagian B no 2e

 2. Selesaikan

 

e.

1/2 ⁵log (10x² - 1) - 2 ⁵log x = 1

⁵log (10x² - 1)^1/2 - ⁵log x² = ⁵log 5

⁵log (10x² - 1)^1/2 / x² =⁵log 5

(10x² - 1)^1/2 / x² = 5

(10x² - 1)^1/2 = 5x²

dikuadratkan agar pangkat 1/2 nya hilang

10x² - 1 = 25x⁴

0 = 25x⁴ - 10x² + 1

0 = (5x² - 1)(5x² - 1)

maka

5x² - 1 =0

5x² = 1

x² = 1/5

x = 1/√5

rasionalkan dengan mengkalikan dengan √5/√5

x = √5 / 5

x = 1/5 √5

Kunci Jawaban Matematika Sukino Kelas X Peminatan Bab 2 LKS 3 Bagian B no 2d

2. Selesaikan

d.

log (x² - 6) + log 2 = 1 + log x

log (x² - 6) . 2 = log 10 + log x

log (2x² - 12) = log 10x

2x² - 12 = 10x

2x² - 10x - 12 = 0

(2x + 2)(x - 6) = 0

maka

2x + 2 = 0

2x = - 2

x = -1

(

tidak termasuk ke dalam HP karena domain logaritma tidak boleh minus : 

(x² - 6) 

= (-1)² - 6 

= 1 - 6 

= -5

)

atau

x - 6 = 0

x = 6

maka HP : x = 6

Kunci Jawaban Matematika Sukino Kelas X Peminatan Bab 2 LKS 3 Bagian B no 2c

2. Selesaikan

c.

⁵log (3x² - 20x + 50) = 2

⁵log (3x² - 20x + 50) = ⁵log 5²

3x² - 20x + 50 = 5²

3x² - 20x + 50 = 25

3x² - 20x + 50 - 25 = 0

3x² - 20x + 25 = 0

(3x - 5)(x - 5) = 0

3x = 5

x = 5/3

atau 

x = 5

 

Kunci Jawaban Matematika Sukino Kelas X Peminatan Bab 2 LKS 3 Bagian B no 2b

 2. Selesaikan

b. 

³log (2x + 1) - ³log (x - 7) = 2

³log ((2x + 1) / (x - 7)) = ³log 3²

(2x + 1) / (x - 7) = 3²

(2x + 1) / (x - 7) = 9

2x + 1 = 9 (x - 7)

2x + 1 = 9x - 63

2x - 9x = - 63 - 1

- 7x = - 64

x = 64/7

x = 9 1/7

Kunci Jawaban Matematika Sukino Kelas X Peminatan Bab 2 LKS 3 Bagian B no 2a

2. Selesaikan

a. 

²log ((3x + 1) / (2x - 7)) = 3

²log ((3x + 1) / (2x - 7)) = ²log 2³

(3x + 1) / (2x - 7) = 2³

(3x + 1) / (2x - 7) = 8

3x + 1 = 8 (2x - 7)

3x + 1 = 16x - 56

3x - 16x = - 56 - 1

-13x = - 57

x = 57/13

x = 4 5/13ipa

Kunci Jawaban Matematika Sukino Kelas X Peminatan Bab 2 LKS 3 Bagian B no 1h

1. Tentukan HP dari setiap persamaan berikut.

h. 

³log (2x +5) - ³log (x² + 4x + 4) = - 2

³log (2x +5) - ³log (x² + 4x + 4) = ³log 3^-2

³log (2x +5) / (x² + 4x + 4) = ³log 1/3²

³log (2x +5) / (x² + 4x + 4) = ³log 1/9

(2x +5) / (x² + 4x + 4) = 1/9

9 (2x + 5) = x² + 4x + 4

18x + 45 = x² + 4x + 4

0 = x² + 4x - 18x + 4 - 45

0 = x² - 14x - 41

gunakan rumus abc untuk melakukan pemfaktoran

- b ± √b² - 4ac

------------------

2a

   14 ± √196 - 4 . 1 . (-41)

= --------------------------------

              2 . 1

   14 ± √196 + 164

= ------------------------

              2

   14 ± √360

= ------------------------

              2 

    14 ± √36√10 

= ------------------------

              2 

    14 ± 6√10 

= ------------------------

              2 

= 7 ± 3 √10

jadi nilai x :

x = 7 + 3√10

atau

x = 7 - 3√10

Kunci Jawaban Matematika Sukino Kelas X Peminatan Bab 2 LKS 3 Bagian B no 1g

 1. Tentukan HP dari setiap persamaan berikut.

g. 

log (x - 1) + log (x - 3) = log (x - 1)

log (x - 1)(x - 3) = log (x - 1)

(x - 1)(x - 3) = (x - 1)

x² - 4x + 3 = x - 1

x² - 5x + 4 = 0

(x - 4)(x - 1) = 0

x = 4

atau

x = 1 (tidak termausk, karena domain logaritma harus > 0)

jadi HP : x = 4

Kunci Jawaban Matematika Sukino Kelas X Peminatan Bab 2 LKS 3 Bagian B no 1f

1. Tentukan HP dari setiap persamaan berikut.

f. 

log (x + 3) - log (x - 1) = log 6

log (x + 3) / (x - 1) = log 6

(x + 3) / (x - 1) = 6

x + 3 = 6 (x - 1)

x + 3 = 6x - 6

x - 6x = - 6 - 3

- 5x = - 9

x = 9/5

Kunci Jawaban Matematika Sukino Kelas X Peminatan Bab 2 LKS 3 Bagian B no 1e

1. Tentukan HP dari setiap persamaan berikut.

e. 

³log (x - 4) + ³log (x + 4) = 2

³log (x - 4)(x + 4) = ³log 3²

³log (x - 4)(x + 4) = ³log 9 

(x - 4)(x + 4) = 9

x² - 16 = 9

x² = 9 + 16

x² = 25

x = 5

Kunci Jawaban Matematika Sukino Kelas X Peminatan Bab 2 LKS 3 Bagian B no 1d

1. Tentukan HP dari setiap persamaan berikut.

d. 

⁴log (4 - x²) = ⁴log (x² - 2)

4 - x² = x² - 2

- x² - x² = - 2 - 4

- 2x² = - 6

x² = 3

x = √3

Kunci Jawaban Matematika Sukino Kelas X Peminatan Bab 2 LKS 3 Bagian B no 1c

1. Tentukan HP dari setiap persamaan berikut.

c. 

log (2x - 1) - log (x - 3) = log 7

log (2x - 1) / (x - 3) = log 7

 (2x - 1) / (x - 3) = 7

2x - 1 = 7 (x - 3)

2x - 1 = 7x - 21

2x - 7x = - 21 + 1

- 5x = - 20

x = -20/-5

x = 4

Kunci Jawaban Matematika Sukino Kelas X Peminatan Bab 2 LKS 3 Bagian B no 1b

 1. Tentukan HP dari setiap persamaan berikut.

b. 

log (x - 2) + log (x - 1) = log 6

log (x - 2)(x - 1) = log 6

(x - 2)(x - 1) = 6

x² - 3x + 2 = 6

x² - 3x + 2 - 6 = 0

x² - 3x - 4 = 0

(x - 4)(x + 1) = 0

x = 4 atau x = -1 (tidak termasuk, karena domain logaritman harus > 0)

maka HP : x = 4

Kunci Jawaban Matematika Sukino Kelas X Peminatan Bab 2 LKS 3 Bagian B no 1a

1. Tentukan HP dari setiap persamaan berikut.

a. 

²log x + ²log (x - 2) = 3

Jawaban :

²log x + ²log (x - 2) = 3

²log x (x - 2) = ²log 2³

²log (x² - 2x) = ²log 8

x² - 2x = 8

x² - 2x - 8 = 0

(x - 4)(x + 2) = 0

x = 4 atau x = - 2 (tidak termasuk karena f(x) harus > 0)

jadi HP : x = 4 

Soal dan Pembahasan Matematika Sukino Kelas X Bab 2 LKS 3 no 20

 Matematika Sukino Kelas X

Bab 2 : Fungsi, Persamaan, dan Pertidaksamaan Logaritma

LKS 3

A.

20. Nilai x yang memenuhi persamaan

³log x . ⁶log x . ⁹log x = ³log x . ⁶log x + ³log x . ⁹log x + ⁶log x . ⁹log x

adalah ...

a. 1/3

b. 1

c. 48

d. 81

e. 162

Jawaban : E

³log x . ⁶log x . ⁹log x = ³log x . ⁶log x + ³log x . ⁹log x + ⁶log x . ⁹log x

³log x . ⁶log x . ^{3^2}log x = ³log x . ⁶log x + ³log x . ^{3^2}log x + ⁶log x . ^{3^2}log x

³log x . ⁶log x . 1/2 . ³log x = ³log x . ⁶log x + ³log x . 1/2 . ³log x + ⁶log x . 1/2 ³log x

1/2 . ³log² x . ⁶log x = ³log x . ⁶log x + 1/2 ³log² x + 1/2 ⁶log x . ³log x

1/2 . ³log² x . ⁶log x = 3/2 ³log x . ⁶log x + 1/2 ³log² x

kalikan dengan 2, agar penyebut nya hilang

³log² x . ⁶log x = 3 ³log x . ⁶log x +  ³log² x

³log² x . ⁶log x = ³log x (3 . ⁶log x +  ³log x)

³log² x . ⁶log x = ³log x (3 . ⁶log x +  ³log x)

³log x . ⁶log x = 3 . ⁶log x +  ³log x

ubah ⁶log x = ³log x / ³log 6

³log x . ⁶log x = 3 . ⁶log x +  ³log x

³log x . ³log x / ³log 6 = 3 . (³log x / ³log 6)+  ³log x

samakan penyebut di ruas kanan

³log x . ³log x / ³log 6 = 3 . (³log x / ³log 6)+  ³log x

³log² x / ³log 6 = (3 . ³log x +  ³log x . ³log 6 ) / ³log 6

kalikan dengan ³log 6 agar penyebutnya hilang

³log² x = 3 . ³log x +  ³log x . ³log 6 

³log² x = ³log x  (3 + ³log 6 )

³log x = 3 + ³log 6

ubah 3 menjadi ³log 3³ 

³log x = 3 + ³log 6

³log x = ³log 3³ + ³log 6

³log x = ³log 27 + ³log 6

³log x = ³log (27 . 6)

x = 27 . 6

x = 162

Soal dan Pembahasan Matematika Sukino Kelas X Bab 2 LKS 3 no 19

Matematika Sukino Kelas X

Bab 2 : Fungsi, Persamaan, dan Pertidaksamaan Logaritma

LKS 3

A.

19. Nilai a yang memenuhi ekspresi :

1/¹⁰log a + 1/^√10log a + 1/^√√10log a + ... = 200

adalah ...

a. 10^-2

b. 10^-1

c. 10^1/2

d. 10^{10^-2}

e. 10^{10^-1}

Jawaban : D

bentuk deret tak hingga

cari dulu rasio nya,

r = U2 / U1

r = (1/^√10log a) / (1/¹⁰log a)

r = (¹⁰log a) / (^√10log a)

r = (¹⁰log a) / (^{10^1/2}log a)

r = (¹⁰log a) / (2 . ¹⁰log a)

r = (¹⁰log a) / (2 . ¹⁰log a)

r = 1/2

rumus untuk menghitung jumlah deret tak hingga :

Sn = a / (1 - r)

Sn = (1/¹⁰log a) / (1 - 1/2)

Sn = (1/¹⁰log a) / (1/2)

Sn = 2/¹⁰log a

200 = 2/¹⁰log a

¹⁰log a = 2/200

¹⁰log a = 1/100

¹⁰log a = 1/10²

¹⁰log a = 10^-2

a = 10^{10^-2}

> soal no 20

Soal dan Pembahasan Matematika Sukino Kelas X Bab 2 LKS 3 no 18

Matematika Sukino Kelas X

Bab 2 : Fungsi, Persamaan, dan Pertidaksamaan Logaritma

LKS 3

A.

18. Misalkan a dan b adalah dua bilangan real berlainan dan keduanya lebih besar dari satu. Banyaknya nilai x yang memnuhi persamaan :

^alog x . ^blog x = ^alog b

adalah ,,,   

a. 0

b. 1

c. 2

d. 3

e. tak hingga

Jawaban : E

diketahui dari soal,

^alog x . ^blog x = ^alog b

^alog x = ^alog b / ^blog x ... (i)

dari sifat logaritma, 

^alog b = ^xlog b /  ^xlog a

^alog b = ^xlog b .  ^alog x

ganti ^alog x dengan (i) 

^alog b = ^xlog b .  ^alog b / ^blog x

^alog b = ^xlog b .  ^alog b / ^blog x

1 = ^xlog b / ^blog x

1 = ^xlog b . ^xlog b

1 = ^xlog² b

^xlog b = 1

x = b

atau 

^xlog b = - 1

x^-1 = b

x = 1/b

dengan b adalah bilangan real dan keduanya lebih besar dari satu, maka banyak nya nilai x yang memenuhi persamaan adalah tak hingga

> soal no 19

Soal dan Pembahasan Matematika Sukino Kelas X Bab 2 LKS 3 no 17

Matematika Sukino Kelas X

Bab 2 : Fungsi, Persamaan, dan Pertidaksamaan Logaritma

LKS 3

A.

17. Diketahui ⁵log ( (5⁴⁰²² - 5⁴⁰¹⁸) / (5⁴⁰²⁰ - 5⁴⁰¹⁶)) = x . Nilai dari ^{x^2}log 1024 adalah ...

a. 2

b. 4

c. 6

d. 8

e. 10

Jawaban : 

diketahui 

⁵log ( (5⁴⁰²² - 5⁴⁰¹⁸) / (5⁴⁰²⁰ - 5⁴⁰¹⁶)) = x

⁵log (5⁴⁰²² - 5⁴⁰¹⁸) - ⁵log(5⁴⁰²⁰ - 5⁴⁰¹⁶) = x

⁵log (5⁴⁰¹⁸ (5⁴ - 1)) - ⁵log(5⁴⁰¹⁶ (5⁴ - 1)) = x

⁵log (5⁴⁰¹⁸ (625 - 1)) - ⁵log(5⁴⁰¹⁶ (625 - 1)) = x

⁵log (5⁴⁰¹⁸ . 624) - ⁵log(5⁴⁰¹⁶ . 624) = x

⁵log 5⁴⁰¹⁸ + ⁵log 624 - (⁵log 5⁴⁰¹⁶ + ⁵log 624) = x

⁵log 5⁴⁰¹⁸ + ⁵log 624 - ⁵log 5⁴⁰¹⁶ - ⁵log 624 = x

⁵log 5⁴⁰¹⁸ - ⁵log 5⁴⁰¹⁶ = x

4018 - 4016 = x

2 = x

x = 2

yang ditanya :

^{x^2}log 1024

= ^{x^2}log 2¹⁰

= 10/2 ^xlog 2

= 5 . ^xlog 2

masukkan nilai x = 2

= 5 . ²log 2

= 5 . 1

= 5

> soal no 18

Soal dan Pembahasan Matematika Sukino Kelas X Bab 2 LKS 3 no 16

Matematika Sukino Kelas X

Bab 2 : Fungsi, Persamaan, dan Pertidaksamaan Logaritma

LKS 3

A.

16. Jika f(n) = ²log 3 . ³log 4 . ⁴log 5 ... ^{n - 1} log n, maka f(8) + f(16) + f(32) + ... + f(2³⁰) = ...

a. 461

b. 462

c. 463

d. 464

e. 465

Jawaban : B

diketahui :

f(n) = ²log 3 . ³log 4 . ⁴log 5 ... ^{n - 1} log n

f(n) = ²log 3 . ³log 4 . ⁴log 5 ... ^{n - 1} log n

f(n) = ²log n

yang ditanya :

f(8) + f(16) + f(32) + ... + f(2³⁰) = ?

²log 8 + ²log 16 + ²log 32 + ... + ²log 2³⁰

²log 2³ + ²log 2⁴ + ²log 2⁵ + ... + ²log 2³⁰

3 + 4 + 5 + ... + 30

jadi bentuk deret... hitung dulu berapa banyak suku nya,

m = (suku terakhir - suku pertama) + 1

m = (30 - 3) + 1

m = 27 + 1

m = 28

rumus menghitung jumlah suku hingga deret ke - m

a = 3

b = selisih deret = 4 - 3 = 1

Sm = m/2 (2a + (m - 1) b)

S28 = 28/2 (2 . 3 + (28 - 1) . 1)

S28 = 14 (6 + 27)

S28 = 14 . 33

S28 = 462

> soal no 17

Soal dan Pembahasan Matematika Sukino Kelas X Bab 2 LKS 3 no 15

Matematika Sukino Kelas X

Bab 2 : Fungsi, Persamaan, dan Pertidaksamaan Logaritma

LKS 3

A.

15. Jika diketahui nilai a . b . c = 2⁶ dan (²log a)(²log bc) + (²log b)(²log c) = 10, dengan a, b, c ≥ 0, maka nilai dari ekspresi

√(²log² a + ²log² b + ²log² c) adalah ...

a. 2

b. 3

c. 4

d. 5

e. 6

Jawaban : C

diketahui 

(²log a)(²log bc) + (²log b)(²log c) = 10

(²log a)(²log b + ²log c) + (²log b)(²log c) = 10

(²log a . ²log b + ²log a ²log c) + (²log b)(²log c) = 10

²log a . ²log b + ²log a ²log c + ²log b ²log c = 10

a . b . c = 2⁶

²log (a . b . c) = 6

²log a + ²log b + ²log c = 6

biar bisa dicocokin sama yang ditanya dan yang di ketahui di atas, selanjutnya kita kuadratin aja

(²log a + ²log b + ²log c)² = 36

²log² a + ²log² b + ²log² c + 2 . ²log a ²log b + 2. ²log a ²log c + 2 . ²log b ²log c = 36

²log² a + ²log² b + ²log² c + 2 (²log a . ²log b + ²log a ²log c + ²log b ²log c) = 36

²log² a + ²log² b + ²log² c + 2 (10) = 36

²log² a + ²log² b + ²log² c + 20 = 36

²log² a + ²log² b + ²log² c = 16

yang ditanya :

√(²log² a + ²log² b + ²log² c)

= √16

= 4

> soal no 16

Soal dan Pembahasan Matematika Sukino Kelas X Bab 2 LKS 3 no 14

Matematika Sukino Kelas X

Bab 2 : Fungsi, Persamaan, dan Pertidaksamaan Logaritma

LKS 3

A.

14. Jika ^blog a = - 2 dan ³log b = (³log 2)(1 + ²log 4a), hasil dari 4a + b = ...

a. 81

b. 72

c. 36

d. 12

e. 3

Jawaban : E

^blog a = - 2

³log b = (³log 2)(1 + ²log 4a)

³log b = ³log 2 + (³log 2 . ²log 4a)

³log b = ³log 2 + (³log 2 . ²log 4a)

³log b = ³log 2 + ³log 4a

³log b = ³log (2 . 4a)

³log b = ³log 8a

b = 8a

^blog a = - 2

b^-2 = a

1/b² = a

1/(8a)² = a

1/64a² = a

1/64 = a³

1/(4³) = a³ 

a = 1/4

nilai dari b :

b = 8a

b = 8 . 1/4

b = 2

nilai dari 4a + b

= 4 . 1/4 + 2

= 1 + 2

= 3

> soal no 15

Soal dan Pembahasan Matematika Sukino Kelas X Bab 2 LKS 3 no 13

 Matematika Sukino Kelas X

Bab 2 : Fungsi, Persamaan, dan Pertidaksamaan Logaritma

LKS 3

A.

13. Diketahui a = ⁴log x dan b = ²log x. Jika ⁴log b + ²log a = 2, maka nilai dari (a + b) adalah ...

a. 4

b. 6

c. 8

d. 12

e. 16

Jawaban : B

diketahui :

a = ⁴log x

4^a = x ... (i)

b = ²log x

2^b = x ... (ii)

dari persamaan (i) dan (ii) diperoleh :

4^a = 2^b

2^2a = 2^b

2a = b

⁴log b + ²log a = 2

^{2^2}log 2a + ²log a = 2

1/2 ²log 2a + ²log a = 2

²log (2a)^1/2 + ²log a = 2

²log ((2a)^1/2. a) = ²log 2²

2^1/2 . a^3/2 = 4

2a³ = 16

a³ = 8

a = 2

hitung nilai b

2a = b

2 . 2 = b

b = 4

nilai dari a + b

= 2 + 4

= 6

> soal no 14

Soal dan Pembahasan Matematika Sukino Kelas X Bab 2 LKS 3 no 12

Matematika Sukino Kelas X

Bab 2 : Fungsi, Persamaan, dan Pertidaksamaan Logaritma

LKS 3

A.

12. Jika ^alog b - ^blog a = -3, maka nilai dari ekspresi (^alog b)² + (^blog a)²  = ...

a. 5

b. 7

c. 9

d. 11

e. 13

Jawaban : D

misalkan :

^alog b = x

^blog a = y

maka,

^alog b - ^blog a = -3

x - y = - 3

(^alog b)² +(^blog a)²

= x² + y²

diubah ke dalam bentuk yang diketahui di atas

**

(x - y)²  = x² + y² - 2xy

agar bentuk ini menjadi x² + y² saja (tanpa - 2xy), maka harus ditambahkan dengan + 2xy

**

= (x - y)² + 2xy

= (-3)² + 2 . ^alog b . ^blog a

= 9 + 2 . ^alog a

= 9 + 2 . 1

= 9 + 2

= 11

> soal no 13

Soal dan Pembahasan Matematika Sukino Kelas X Bab 2 LKS 3 no 11

Matematika Sukino Kelas X

Bab 2 : Fungsi, Persamaan, dan Pertidaksamaan Logaritma

LKS 3

A.

11. Diketahui ³log a - 2 (³log b) ≤ 1 dan ³log b - 2 (³log a) = - 2.

Nilai dari eksporesi (a x b) adalah ...

a. 1

b. 2

c. 3

d. 4

e. 9

Jawaban : C

³log a - 2 (³log b) = 1

³log a - ³log b² = 1

³log (a/b²) = 1 ... (i)

³log b - ³log a² = - 2

³log (b/a²) = - 2 ... (ii)

jumlahkan (i) dan (ii)

³log (a/b²) = 1

³log (b/a²) = - 2

---------------------- +

³log (a/b²) + ³log (b/a²) = 1+ (-2)

³log (a/b² . b/a²) = - 1

³log (1/ab)= -1

³log (ab)^-1 = -1

- 1 . ³log (ab)= -1

³log (ab)= 1

3¹ = ab

a x b = 3

> soal no 12

Soal dan Pembahasan Matematika Sukino Kelas X Bab 2 LKS 3 no 10

Matematika Sukino Kelas X

Bab 2 : Fungsi, Persamaan, dan Pertidaksamaan Logaritma

LKS 3

A.

10. Jika ⁹log a = - 1 dan ^1/alog x = 1/2, maka nilai x adalah ...

a. 1

b. 2

c. 3

d. 4

e. 9

Jawaban : C

⁹log a = - 1

9^-1 = a

a = 1/9

a = 3^-2

^1/alog x = 1/2

^{a^ -1} log x = 1/2

- 1 . ^a log x = 1/2

- ^{3^-2}log x = 1/2

- (- 1/2) . ³ log x = 1/2

1/2 . ³log x = 1/2

³log x = 1

3¹ = x

x = 3

> soal no 11

Soal dan Pembahasan Matematika Sukino Kelas X Bab 2 LKS 3 no 9

Matematika Sukino Kelas X

Bab 2 : Fungsi, Persamaan, dan Pertidaksamaan Logaritma

LKS 3

A.

9. Jika ²log (xy) = 7 dan ²log (x²/y) = 5, maka x + y = ...

a. 32

b. 28

c. 24

d. 20

e. 16

Jawaban : C

²log (xy) = 7

²log x + ²log y = 7 ... (i)

²log (x²/y) = 5

²log x² - ²log y = 5

2 ²log x - ²log y = 5 ... (ii)

lakukan eliminasi (i) dan (ii)

²log x + ²log y = 7

2 ²log x - ²log y = 5

-------------------------- + 

3 ²log x = 7 + 5

3 ²log x = 12

²log x = 12/3

²log x = 4

2⁴ = x

x = 16

masukkan ke dalam persamaan (i)

²log x + ²log y = 7

4 + ²log y = 7

²log y = 7 - 4

²log y = 3

2³ = y

y  = 8

maka nilai dari

x + y

= 16 + 8

= 24

> soal no 10

Soal dan Pembahasan Matematika Sukino Kelas X Bab 2 LKS 3 no 8

Matematika Sukino Kelas X

Bab 2 : Fungsi, Persamaan, dan Pertidaksamaan Logaritma

LKS 3

A.

8. Jika ²log x +  ³log (x + y) = 5 dan ²log x - ³log (x + y) = 1, maka x + y = ....

a. 5

b. 6

c. 7

d. 8

e. 9

Jawaban : E

²log x +  ³log (x + y) = 5 ... (i)

²log x - ³log (x + y) = 1 ... (ii)

lakukan eliminasi dari persamaan (i) dan (ii)

²log x +  ³log (x + y) = 5

²log x - ³log (x + y) = 1

---------------------------------- -

³log (x + y) + ³log (x + y) = 5 - 1

2 . ³log (x + y) = 4

³log (x + y) = 2

3² = x + y

x + y = 9

> soal no 9

Soal dan Pembahasan Matematika Sukino Kelas X Bab 2 LKS 3 no 7

 Matematika Sukino Kelas X

Bab 2 : Fungsi, Persamaan, dan Pertidaksamaan Logaritma

LKS 3

A.

7. Jika ^2√2log 9 = k, maka  ²⁷log 4 = ....

a. k/2

b. 8k/9

c. 1/2k

d. 8/9k

e. 9/8k

Jawaban : D

^2√2log 9 = k

^{2 . 2^1/2} log 3² = k

^{2^3/2} log 3² = k

2 / (3/2) .  ² log 3 = k

2 . 2/3 . ²log 3 = k

4/3 . ²log 3 = k

²log 3 = k/(4/3)

²log 3 = 3k/4

²⁷log 4

= ^{3^3}log 2²

= 2/3 ³log 2

= 2/3 . 1/²log 3

= 2/3 . 1/(3k/4)

= 2/3 . 4/3k

= 8/9k

> soal no 8

Soal dan Pembahasan Matematika Sukino Kelas X Bab 2 LKS 3 no 6

Matematika Sukino Kelas X

Bab 2 : Fungsi, Persamaan, dan Pertidaksamaan Logaritma

LKS 3

A.

6. Nilai x yang memenuhi persamaan :

log (x² - 1) - log (x - 1) = 1 + log (x - 8) adalah ...  

a. 9

b.  8

c. 7

d. 6

e. 5

Jawaban : A

log (x² - 1) - log (x - 1) = 1 + log (x - 8)

log ((x² - 1) / (x - 1)) = log 10 + log (x - 8)

log ((x - 1)(x + 1) / (x - 1)) = log (10 . (x - 8))

log (x + 1) = log (10x - 80)

x + 1 = 10x - 80

x - 10x = - 80 - 1

- 9x = - 81

x = - 81 / - 9

x = 9

> soal no 7

Soal dan Pembahasan Matematika Sukino Kelas X Bab 2 LKS 3 no 5

Matematika Sukino Kelas X

Bab 2 : Fungsi, Persamaan, dan Pertidaksamaan Logaritma

LKS 3

A.

5. Nilai x yang memenuhi persamaan :

²log (x² - 2x + 1) = 0 adalah ...  

a. - 1 atau 1

b. - 1 atau 2

c. 0 atau 1

d. 0 atau 2

e. 1 atau 2

Jawaban : D

²log (x² - 2x + 1) = 0

2⁰ = x² - 2x + 1

1 = x² - 2x + 1

0 = x² - 2x + 1 - 1

0 = x² - 2x

0 = x (x - 2)

x = 0

atau 

x = 2

> soal no 6

Soal dan Pembahasan Matematika Sukino Kelas X Bab 2 LKS 3 no 4

 Matematika Sukino Kelas X

Bab 2 : Fungsi, Persamaan, dan Pertidaksamaan Logaritma

LKS 3

A.

4. Diketahui f(x) = ²log x³ - 6, maka f(x) = 12 dipenuhi oleh nilai x = ...  

a. 16

b. 21

c. 36

d. 64

e. 68

Jawaban : D

f(x) = ²log x³ - 6

12 = ²log x³ - 6

12 + 6 = ²log x³

18 = ²log x³

18 = 3 ²log x

18/3 = ²log x

6 = ²log x

²log 2⁶ = ²log x

²log 64 = ²log x

64 = x

x = 64

> soal no 5

Soal dan Pembahasan Matematika Sukino Kelas X Bab 2 LKS 3 no 3

Matematika Sukino Kelas X

Bab 2 : Fungsi, Persamaan, dan Pertidaksamaan Logaritma

LKS 3

A.

3. Jika 2 . ³log y = ³log (x + 1) + 2, maka ...

a. y = x + 3

b. y = 3x + 3

c. y² = - 9 (x + 1)

d. y² = 9 (x + 1)

e. y² = 3 (x + 1)

Jawaban : D

2 . ³log y = ³log (x + 1) + 2

³log y² = ³log (x + 1) + ³log 3²

³log y² = ³log (x + 1) + ³log 9

³log y² = ³log (9(x + 1))

y² = 9 (x + 1)

> soal no 4

Soal dan Pembahasan Matematika Sukino Kelas X Bab 2 LKS 3 no 2

Matematika Sukino Kelas X

Bab 2 : Fungsi, Persamaan, dan Pertidaksamaan Logaritma

LKS 3

A.

2. Nilai x yang memenuhi persamaan :

²log (x² - 5x + 8) = 1 adalah ...

a. 1 atau 2

b. 2 atau 3

c. 3 atau 4

d. 4 atau 5

e. 5 atau 6

Jawaban : B

²log (x² - 5x + 8) = 1

2¹ = x² - 5x + 8

2 = x² - 5x + 8

0 = x² - 5x + 8 - 2

0 = x² - 5x + 6

0 = (x - 3)(x - 2)

x = 3

atau

x = 2

> soal no 3

Soal dan Pembahasan Matematika Sukino Kelas X Bab 2 LKS 3 no 1

Matematika Sukino Kelas X

Bab 2 : Fungsi, Persamaan, dan Pertidaksamaan Logaritma

LKS 3

A.

1. Nilai x yang memenuhi persamaan :

^xlog (3x + 10) = 2 adalah ...

a. 3

b. 4

c. 5

d. 6

e. 7

Jawaban : C

^xlog (3x + 10) = 2

x² = 3x + 10

x² - 3x - 10 = 0

(x - 5)(x + 2) = 0

x = 5 atau x = - 2

yang ada di pilihan jawaban : x = 5

> soal no 2

Soal dan Pembahasan Tes Formatif 2 Eksponensial Kelas X no 13

13. Nilai x yang memenuhi pertidaksamaan (√5)^{x^3} < 25^{x^2 - 3/4 x} adalah ...

a. 1 < x < 3 atau x > 4

b. 0 < x < 1 atau x > 2

c. 0 < x < 3 atau x > 4

d. 1 < x < 3 atau x > 0

e. 0 < x < 1 atau x > 3

Jawaban : D

Soal dan Pembahasan Tes Formatif 2 Eksponensial Kelas X no 12

12. Bila 4/5 (2^{3x - 2}+ 8^x/20 = 1, maka x = ...

a. 3/2

b. 2/3

c. - 2/3

d. - 3/2

e. 1

Jawaban : B

Soal dan Pembahasan Tes Formatif 2 Eksponensial Kelas X no 11

11. Akar - akar persamaan 3^{2x + 1} - 28 . 3^x + 9 = 0 adalah x₁ dan x₂ dimana x₁ > x₂

maka 3x₁ - x₂ = ,,,

a. - 5

b. - 1

c. 4

d. 3

e. 9

Jawaban :

Soal dan Pembahasan Tes Formatif 2 Eksponensial Kelas X no 10

10. Nilai x yang memenuhi persamaan (x² + 1) ^{x^2 + 1} = (x² + 1) ^{x^2 + x + 4} adalah ... 

a. x = 0, x = 3

b. x = -3, x = 3

c. x = - 1, x = 3

d. x = - 3, x = -1

e. x = 0, x = -3

Jawaban : E

Soal dan Pembahasan Tes Formatif 2 Eksponensial Kelas X no 9

9. Jika x dan y yang memenuhi sistem persamaan

2^{x + 1} - 3^y = 7

- 2^{x - 1} + 3^{y + 1} = 1

maka nilai x² - y² adalah ...

a. 0

b. 2

c. 4

d. 6

e. 8

Jawaban : C

Soal dan Pembahasan Tes Formatif 2 Eksponensial Kelas X no 8

8. Batas nilai x yang memenuhi pertidaksamaan

3^{-2x + 5} - 730 . 3^-x  + 3 < 0 adalah ... 

a. - 1 < x < 5

b. x < -1 atau x > 5

c. - 5 < x < 1

d. 1/243 < x < 3

e. x < 1 atau x > 3

Jawaban : A

Soal dan Pembahasan Tes Formatif 2 Eksponensial Kelas X no 7

7. Himpunan penyelesaian pertaksamaan 2√4^{x^2 - 3x + 2} < ³√(1/2)^{3 - 6x} adalah ...  

a. {x | x > 3}

b. {x | x > 2}

c. {x | x < 1}

d. {x | 1 < x <4}

e. {x | 2 ≤ x ≤ 3}

Jawaban : D

Soal dan Pembahasan Tes Formatif 2 Eksponensial Kelas X no 6

6. Jika 8^m = 27, maka 2 . 4^m - 2^{m + 1} = ...

a. 12

b. 15

c. 18

d. 21

e. 24

Jawaban : A

Soal dan Pembahasan Tes Formatif 2 Eksponensial Kelas X no 5

5. Jumlah nilai x yang memenuhi 8^{5x^2 + 4x} = 4^{10x^2 - 9x + 6} adalah ...

a. 

b. 2

c. 3

d. 4

e. 5

Jawaban :

Soal dan Pembahasan Tes Formatif 2 Eksponensial Kelas X no 4

4. Jika x = 2 - √3 , maka 3^{x^2 - 4x} = 

a. 0

b. 1/3

c. 3

d. 3√3

e. 3^{1 + √3} 

Jawaban : B

Soal dan Pembahasan Tes Formatif 2 Eksponensial Kelas X no 3

3. Himpunan penyelesaian dari 2^{x + 5} < 2^{x^2 + 6x + 11} adalah ... 

a. {x | x < -3 atau x > - 2}

b. {x | x < 2 atau x > 3}

c. {x | x < -6 atau x > -1}

d. {x | - 3 < x < 2}

e. {x | 2 < x < 3}

Jawaban :

Soal dan Pembahasan Tes Formatif 2 Eksponensial Kelas X no 2

2. Diketahui :

2 . 4^x + 2^{3 - 2x} = 17

Nilai dari 2^2x = ...

a. 1/2 atau 8

b. 1/2 atau 4

c. 1/2 √2 atau 2√2 

d. 1/2 atau 1/2 √2

e. 1 atau 4

Jawaban : A

Soal dan Pembahasan Tes Formatif 2 Eksponensial Kelas X no 1

 1. Akar dari persamaan 3^{5x - 1} = 27^{x + 3} ... 

a. 1

b. 2

c. 3

d. 4

e. 5

Jawaban : E

Soal dan Pembahasan Eksponensial Soal Subjektif

11. 

2^{(2x^2 + 9x)} > 1/32

Jawaban :

12.

(1/2)^{x^2} ≤ (1/4)^{4x + 6}

Jawaban :

13.

(1/8)^{2x - x^2} ≤ 2^{x^2 - 3x + 5}

Jawaban : 

14.

(x² - 2x + 3)^{2x + 1} ≤ (x² - 2x + 3)^{x + 3}

Jawaban :

15.

6^{(2x + 1)} - 8 . 6^x + 8 ≤ 0

Jawaban :

Soal dan Pembahasan Soal Objektif Eksponensial Kelas X no 10

10. Himpunan penyelesaian pertaksamaan 2√4^{x^2 - 3x + 2} < ³√(1/2)^{3 - 6x} adalah ...

a. {x | x > 3}

b. {x | x > 2}

c. {x | x < 1}

d. {x | 1 < x < 4}

e. {x | 2 ≤ x ≤ 3}

Jawaban : D

Soal dan Pembahasan Soal Objektif Eksponensial Kelas X no 9

9. Batas-batas x yang memenuhi 

(0,25)^{3x - x^2} - 2^{15 - 2x - x^2} ≤ 0 adalah ...

a. x ≤ - 3 atau x ≥ 5/3

b. x ≤ - 5/3 atau x ≥ 3

c. - 5/3 ≤ x ≤ 3

d. - 5 ≤ x ≤ 3

e. - 3 ≤ x ≤ 5

Jawaban : C

Soal dan Pembahasan Soal Objektif Eksponensial Kelas X no 8

8. Batas-batas x yang memenuhi 

√(1/27^2x) > (9^x)³ / 81^{3 - x} adalah ...

a. x < 4

b. x < 3

c. x < 2

d. x < 1

e. x > - 1

Jawaban : D

Soal dan Pembahasan Soal Objektif Eksponensial Kelas X no 7

7. Penyelesaian dari pertidaksamaan :

(1/3)^{2x + 1} > √(27/3^{x - 1}) adalah ...

a. x > 5/6

b. x < - 6/5

c. x > - 5/6

d. x < 2

e. x < - 2

Jawaban : E

Soal dan Pembahasan Soal Objektif Eksponensial Kelas X no 6

6. Batas-batas nilai x yang memenuhi 49^{2 - 3x} < 1/243 adalah ...

a. x < 5/6

b. x > 7/6

c. x < 7/6

d. x > 5/6

e. x > - 7/6

Jawaban : B

49^{2 - 3x} < 1/243

7^{2(2 - 3x)} < 3^-5

*karena bilangan pokoknya berbeda, maka tidak ada jawabannya.. jika soalnya diubah menjadi :

49^{2 - 3x} < 1/343

7^{2(2 - 3x)} < 7^-3

2(2 - 3x) < - 3

4 - 6x < - 3

- 6x < - 3 - 4

- 6x < - 7

x > 7/6

Soal dan Pembahasan Pertidaksamaan Eksponensial Soal Menjodohkan

 A. Soal Menjodohkan

Pasangkan himpunan penyelesaian dari pertidaksamaan berikut dengan jawaban yang benar !

Soal :

1. (1/2)^{x^2 + 2x - 8} > (1/2)^{x - 2}

2. 6^{x^2 - x - 5} < 6^{x - 2}

3. 2^2x  - 3 . 2^2x + 8 > 0

4. 3^{x^2 - 2x - 5} < 27

5. 2^{3 - 2x} + 2 > 17 / 2^x

Pilihan HP :

A. {x | x < 1 atau x > 2}

B. {x | - 2 < x < 4}

C. {x | - 1 < x < 3}

D. {x | x < -1 atau x > 3}

E. {x | - 3 < x < 2}

Jawaban :

Jawaban Soal Matematika Kelas X Eksponensial Soal Tingkat Sulit no 5

Soal Matematika Kelas X

Eksponensial

Tingkat Sulit

5. Jika a^x = b^y = c^z dan b² = ac, maka ...

a. 2yz / (y + z)

b. 2yz / (2z - y)

c. 2yz / (2y - z)

d. yz / (2y - z)

e. yz / (2z - y)

Jawaban : E

Jawaban Soal Matematika Kelas X Eksponensial Soal Tingkat Sulit no 4

Soal Matematika Kelas X

Eksponensial

Tingkat Sulit

4. Jika 4^x - 4^{x - 1} 6, maka (2x)^x sama dengan ... .

a. 3

b. 3√3

c. 9

d. 9√3 

e. 27

Jawaban : B

Jawaban Soal Matematika Kelas X Eksponensial Soal Tingkat Sulit no 3

Soal Matematika Kelas X

Eksponensial

Tingkat Sulit

3. Jika 2^{(x + 2)} + 4^{(x + 1)} = 48 , nilai dari 1 / (1 + x) = ...

a. ³log 2

b. 1/14

c. ²log 3

d. ²log 6

e. 3

Jawaban :

2^{(x + 2)} + 4^{(x + 1)} = 48

2^x 2² + 2^{2(x + 1)} = 48

2^x 2² + 2^2x 2² = 48

misalkan a = 2^x

2^x 2² + 2^2x 2² = 48

4a + 4a² = 48

4a² + 4a - 48 = 0

(2a - 6)(2a + 8) = 0

2a = 6

a = 3

atau

2a = - 8

a = - 4

(ini tidak mungkin diperoleh x, karena negatif... 2^x = - 4 , ga ada pangkat yang bisa menghasilkan 2 menjadi negatif)

jadi yang tersisa : a = 3

2^x = 3

x = ²log 3

nilai dari 

1 / (1+x)

= 1 / (1 + ²log 3)

ubah 1 yang ada di penyebut menjadi ²log 2

= 1 / (²log 2 + ²log 3)

= 1 / (²log 6)

= ⁶log 2

** tidak ada di pilihan jawaban**

Jawaban Soal Matematika Kelas X Eksponensial Soal Tingkat Sulit no 2

Soal Matematika Kelas X

Eksponensial

Tingkat Sulit

2. Himpunan penyelesaian dari persamaan (x² - 2x - 2)^{x^2 - 3x + 2} = (x² - 2x - 2)^{2x - 4} adalah ... 

a. {- 1, 2, 3}

b. {- 1, 1, 1 - √2, 2 , 1 + √2}

c. {- 1, 1 - √3, 1 - √2, 2 , 1 + √2, 1 + √3, 3}

d. {- 1, 1, 1 - √2, 2 , 1 + √2, 3}

e. {- 1, 2, 1 + √3, 3}

Jawaban : E

(x² - 2x - 2)^{x^2 - 3x + 2} = (x² - 2x - 2)^{2x - 4}

syarat :

(i)

x² - 3x + 2 = 2x - 4

x² - 3x - 2x + 2 + 4 = 0

x² - 5x + 6 = 0

(x - 2)(x - 3) = 0

x = 2 atau x = 3

(ii)

x² - 2x - 2 = 1

x² - 2x - 2 - 1 = 0

x² - 2x - 3 = 0

(x - 3)(x + 1) = 0

x = 3 atau x = - 1

(iii)

x² - 2x - 2 = - 1

x² - 2x - 2 + 1 = 0

x² - 2x - 1 = 0

tidak ada yang termasuk HP

(iv)

x² - 2x - 2 = 0

yang termasuk HP dari syarat (iv) = 1 + √3

HP gabungan dari syarat (i) sampai (iv) :

{- 1, 2, 1 + √3, 3}

Jawaban Soal Matematika Kelas X Eksponensial Soal Tingkat Sulit no 1

Soal Matematika Kelas X

Eksponensial

Tingkat Sulit

1. Jumlah akar-akar persamaan 5^{x + 1} + 5^{1 - x} = 11 adalah ...

a. 6

b. 5

c. 0

d. - 2

e. - 4

Jawaban :

Jawaban Soal Tingkat Sedang MTKP Kelas X IPA Latihan 1 no 5

Soal Tingat Sedang

MTKP

Persamaan dan Pertidaksamaan Eksponen 

5. Nilai x yang memenuhi 

5^{x + y} = 49

x - y = 6

adalah ...

a. 3 + 1/2 ⁵log7

b. 3 + ⁵log7

c. 49 + ⁵log6

d. 6 ⁵log49

e. 1/2 (3 + ⁵log7)

Jawaban :

Jawaban Soal Tingkat Sedang MTKP Kelas X IPA Latihan 1 no 4

Soal Tingat Sedang

MTKP

Persamaan dan Pertidaksamaan Eksponen 

4. Nilai x yang memenuhi 8^{x + 1} = 24^{x - 1} adalah ...

a. 1 + 6 ²log3

b. 1 + 4 ²log3

c. 1 + 6 ³log2

d. 1 + 6 ⁵log2

e. 1 + 4 ³log2

Jawaban :

Jawaban Soal Tingkat Sedang MTKP Kelas X IPA Latihan 1 no 3

Soal Tingat Sedang

MTKP

Persamaan dan Pertidaksamaan Eksponen 

3. Nilai x yang memenuhi persamaan 4^x - 2^{2x + 1} + 3 = 0 adalah ...

Jawaban :

Jawaban Soal Tingkat Sedang MTKP Kelas X IPA Latihan 1 no 2

Soal Tingat Sedang

MTKP

Persamaan dan Pertidaksamaan Eksponen 

2. Jumlah akar - akar persamaan 5^{x + 1} + 5^{x - 1} = 11 adalah ...

Jawaban :

Jawaban Soal Tingkat Sedang MTKP Kelas X IPA Latihan 1 no 1

Soal Tingat Sedang

MTKP

Persamaan dan Pertidaksamaan Eksponen 

1. Jika anggota Himpunan penyelesaian dari persamaan (x + 1)^{x^2 + 7x + 10} = (2x + 3)^{x^2 + 7x + 10} dijumlahkan, hasilnya adalah ...

Jawaban :