Soal matematika kelas XI IPA SMA Negeri nomor 6

 6. Nilai maksimum dari f(x,y) = 8x + 2y pada daerah yang diarsir berikut ini adalah ...

A. 10

B. 38

C. 56

D. 25

E. 42

Jawaban :

Soal matematika kelas XI IPA SMA Negeri nomor 5

 5. Nilai maksimum dari f (x, y) = 3x + 4y untuk sistem pertidaksamaan x + y ≤ 6, 2x + 3y ≤15. x ≥ 0, dan y ≥ 0 adalah ...

A. 16

B. 17

C. 20

D. 21

E. 25

Jawaban :

Soal matematika kelas XI IPA SMA Negeri nomor 4

 4. Sistem pertidaksamaan untuk daerah penyelesaian berikut ini adalah ...

A. 3x + 5y ≤ 30, 8x + 5y ≤ 40, x ≥ 0, y ≥ 0

B. 3x + 5y ≤ 15, 8x + 5y ≤ 20, x ≥ 0, y ≥ 0

C. 3x + 5y ≥ 30, 8x + 5y ≥ 40, x ≥ 0, y ≥ 0

D. 3x + 5y ≥ 15, 8x + 5y ≥ 20, x ≥ 0, y ≥ 0

E. 3x + 5y ≤ 15, 8x + 5y ≤ 40, x ≥ 0, y ≥ 0

Jawaban :

\

Soal matematika kelas XI IPA SMA Negeri nomor 3

3. Daerah yang diarsir pada gambar berikut ini merupakan himpunan penyelesaian sistem pertidaksamaan …

A. x + 2y ≤ 6 , 2x + y ≤ 6, x + y ≥ 6

B. x + 2y ≤ 6 , 2x + y ≤ 6, x + y ≤ 6

C. x + 2y ≥ 6 , 2x + y ≥ 6, x + y ≥ 6

D. x + 2y ≤ 6 , 2x + y ≥ 6, x + y ≥ 6

E. x + 2y ≥ 6 , 2x + y ≥ 6, x + y ≤ 6

Jawaban :

Soal matematika kelas XI IPA SMA Negeri nomor 2

2. Suatu perusahaan gula memerlukan 400kg unsur A dan 500kg unsur B per minggu. Gula jenis I memerlukan 10kg unsur A dan 20kg unsur B sedangkan gula jenis II memerlukan 15kg unsur A dan 5kg unsur B. Bila keuntungan gula jenis I adalah Rp 1.000 per kg dan gula jenis II adalah Rp 750 per kg, maka keuntungan maksimum per minggu yang diperoleh perusahaan itu adalah Rp …

A. 31.000

B. 33.000

C. 25.000

D. 20.500

E. 40.000

Jawaban :

Soal matematika kelas XI IPA SMA Negeri nomor 1

1. Luas daerah parkir 500m^2. Luas rata-rata mobil sedan adalah 5m^2 dan bus 20m^2. Biaya parkir masing-masing adalah Rp 500 untuk sedan dan Rp 1.000 untuk bus. Daerah parkir itu dapat menampung tidak lebih dari 70 kendaraan. Pendapatan maksimum tukang parkir itu adalah … Rp

A. 40.000

B. 80.000

C. 85.000

D. 25.000

E. 35.000

Jawaban :

Soal Ujian Tingkat SMA / SMK Kelas 12 Matematika Wajib no 35

 35. Perhatikan tabel distribusi frekuensi berikut!

Dari data tersebut, tentukan nilai modusnya !

Jawaban :

Nilai modus adalah nilai yang paling sering muncul, yang dalam hal ini terdapat pada kelas yang memiliki nilai frekuensi terbesar, yaitu kelas nilai 49 -  57

Mo = tb + (d1/(d1 + d2)) p

Dengan Mo = modus

Tb = batas bawah kelas modus

D1 = selisih frekuensi kelas modus dengan kelas sebelumnya

D2 = selisih frekuensi kelas modus dengan kelas setelahnya

P = panjang kelas

Dalam hal ini, 

Tb = 48.5

D1 = 12 - 4 = 8

D2 = 12 - 10 = 2

P = (57-49) + 1 = 9

Mo = 48,5 + 8 / (8+2) .  9

Mo = 48.5 + 8/10 . 9

Mo = 48.5 + 7.2

Mo = 55.7

Soal Ujian Tingkat SMA / SMK Kelas 12 Matematika Wajib no 34

 34. Pusat lingkaran L terletak pada titik potong antara garis 3x + 2y - 21= 0 dengan garis y - 3 = 0. Jika lingkaran tersebut berjari jari 5, tentukan persamaan lingkaran tersebut !

Jawaban :

Soal Ujian Tingkat SMA / SMK Kelas 12 Matematika Wajib no 33

33. Pesawat penumpang mempunyai tempat duduk 48 kursi. Setiap penumpang kelas utama boleh membawa bagasi 60kg, sedangkan kelas ekonomi 20 kg. Daya tampung maksimum bagasi 1800 kg. Harga tiket kelas utama Rp 150.000,- dan kelas ekonomi Rp 100.000,-. Jika semua kursi terisi penuh, maka berapa hasil penjualan tiket maksimum ?

Jawaban :

Soal Ujian Tingkat SMA / SMK Kelas 12 Matematika Wajib no 32

 32. Akar-akar persamaan kuadrat x^2 + (a - 1)x + 2 = 0 adalah x1 dan x2 dimana keduanya positif. Jika x1 = 2 x2, tentukan nilai a !

Jawaban :

x^2 + (a - 1)x + 2 = 0

A = 1

B = a - 1

C = 2

Dengan x1 = 2x2

Ketentuan persamaan kuadrat :

x1 + x2 = - b/a

2x2 + x2 = - (a - 1) / 1

3x2 = 1 - a

X2 = (1- a)/3

X1 . X2 = c/a

2x2. X2 = 2/1

2x2^2 = 2

X2^2 = 1

X2 = 1 atau x2 = -1

Karena kedua akar disebut memiliki bilangan positif, maka x2 = 1

Maka,

X2 = (1- a)/3

Untuk x2 = 1

1 = (1 - a) / 3

3 = 1 - a

A = - 2

Jadi nilai a yang memenuhi persamaan tersebut adalah a = - 2

Soal Ujian Tingkat SMA / SMK Kelas 12 Matematika Wajib no 31

 31. Sebuah lingkaran dipotong menjadi 6 buah juring yang sudut-sudut pusatnya membentuk barisan aritmatika. Diketahui bahwa sudut pusat terbesarnya adalah empat kali sudut pusat terkecil. Tentukan besar sudut pusat terkecil dari juring tersebut! Buatlah langkah penyelesaiannya !

Jawaban :

6 buah juring membentuk barisan aritmatika, dengan sudut terbesarnya (U6) adalah 4x sudut pusat terkecil (U1)

U6 = 4 . U1

Ditanya : U1 ?

Total sudut lingkaran adalah 360

Un = U1 + ( n - 1).b

U6 = U1 + (6 - 1) .b

4U1 = U1 + 5b

3U1 = 5b

b = 3/5 U1

Total sudut = Sn

Sn = 1/2 n (2a + (n - 1) .b)

S6 = 1/2 . 6 . (2. U1 + (6 - 1).3/5 U1)

360 = 3 (2 U1 + 5 . 3/5 U1)

360 / 3 = 2 U1 + 3U1

120 = 5U1

U1 = 120/5

U1 = 24

Sudut terkecil dari juring lingkaran tersebut adalah 24°

Soal Ujian Tingkat SMA / SMK Kelas 12 Matematika Wajib no 30

30. Sebuah dadu dilempar sekali, nilai kemungkinan dadu menunjukkan angka 3 atau lebih adalah ...

a. 1/6

b. 1/2

c. 2/3

d. 1/12

e. 1/36

Jawaban :

angka 3 atau lebih : 3, 4, 5, 6

terdapat 4 kemungkinan angka yang muncul dari total 6 angka pada dadu

maka kemungkinan dadu menunjukkan angka 3 atau lebih adalah :

4 /6

= 2/3

Jawaban : C

Soal Ujian Tingkat SMA / SMK Kelas 12 Matematika Wajib no 29

29. Dari 8 siswa putra dan 4 siswa putri akan diambil secara acak 3 orang siswa untuk menjadi delegasi sekolah dalam suatu acara. Peluang terbentuknya delegasi yang ketiga anggotanya putra semua adalah ...

a. 28.55

b. 17/55

c. 14/55

d. 11/55

e. 9/55

Jawaban :

terdapat 8 putra dan 4 putri, total 12 orang

akan dibentuk 3 orang sebagai delegasi.

Peluang terbentuknya delegasi yang terdiri dari 3 orang putra :

8C3 = 8! / (3! (8 - 3)!)

8C3 = 8! / (3! . 5!)

8C3 = (8 . 7. 6. 5!) / (3! . 5!)

8C3 = (8 . 7 . 6) / 3!

8C3 = (8 . 7 . 6) / (3 . 2. 1)

8C3 = (8 . 7 . 6) / 6

BC3 = 8 . 7

8C3 = 56

kemungkinan keseluruhan

12C3 = 12! / (3! . (12 - 3)!

12C3 = 12! / 3! . 9!

12C3 = (12 . 11 . 10) / 3!

12C3 = 12 . 11. 10 / 6

12C3 = 2 . 11 . 10

12C3 = 220

maka peluang terbentuknya ketiga siswa di dalam delegasi :

8C3 / 12C3

= 56/220

= 14/55

Jawaban : C

Soal Ujian Tingkat SMA / SMK Kelas 12 Matematika Wajib no 28

28. Banyak bilangan genap yang terdiri dari 3 angka berbeda yang dapat disusun dari angka 0,2, 3, 4, 5, 6, dan 7 adalah ...

a. 210

b. 120

c. 105

d. 40,90

4. 75

Jawaban :

bilangan genap dengan 3 angka berbeda :

angka satuan (angka terakhir) dapat berupa angka : 0, 2, 4, 6 (4 pilihan angka)

angka ratusan dapat berupa angka : 0,2,3,4,5,6,7 namun 1 angka telah digunakan untuk angka satuan, sehingga terdapat 6 pilihan angka

angka puluhan dapat berupa angka : 0,2,3,4,5,6,7 namun 2 angka telah digunakan untuk angka satuan dan ratusan, sehingga terdapat 5 pilihan angka

sehingga banyaknya bilangan genap yang terdiri dari 3 angka berbeda :

6 x 5 x 4 = 120

Jawaban : B

Soal Ujian Tingkat SMA / SMK Kelas 12 Matematika Wajib no 27

27. Seorang petugas perpustakaan akan membuat label buku-buku koleksi baru perpustakaan itu. Karena buku-buku tersebut merupakan novel ia menggunakan kode N, dilanjutkan dengan empat angka berbeda dari angka-angka 2, 3, 4, 5,6 dan 7. Banyak label yang dapat disusun petugas perpustakaan tersebut adalah ...

a. 120

b. 180

c. 240

d. 250

e. 360

Jawaban :

susunan empat angka berbeda dari angka :

2, 3, 4, 5, 6, 7

ada 6 pilihan angka yang dapat mengisi dari susunan empat angka tersebut

Angka pertama : 6 pilihan angka

Angka kedua : 5 pilihan angka tersisa (1 angka telah digunakan sebelumnya)

Angka ketiga : 4 pilihan angka tersisa (2 angka telah digunakan sebelumnya)

Angka keempat : 3 pilihan angka tersisa (3 angka telah digunakan sebelumnya)

maka banyak label yang dapat disusun :

6 . 5 . 4. 3

= 30 . 12

= 360

Jawaban : E

Soal Ujian Tingkat SMA / SMK Kelas 12 Matematika Wajib no 26

26. Lima siswa mengikuti ujian susulan. Kelima tersebut mendapatkan nilai 4, 7, 7, 8, dan 9. Standar deviasi dari data nilai susulan kelima siswa tersebut adalah ...

a . √(6/5)

b. √(7/5)

c. √(14/5)

d. √14

e. 14

Jawaban :

Jawaban : C

Soal Ujian Tingkat SMA / SMK Kelas 12 Matematika Wajib no 25

 25. Diketahui data yang disajikan dalam bentuk tabel berikut

Nilai quartil ketiga data tersebut adalah ...

a. 62,75

b. 63,25

c. 94,50

d. 85,79

e. 86,29

Jawaban :

Frekuensi kumulatif
3

9

17

27

34

40
Jumlah data = jumlah frekuensi = 40

Qi = bi + ( (i/4 . N - F) / f ) . l

bi = tepi bawah kuartil
N = jumlah data
F = frekuensi kumulatif sebelum kuartil
f = frekuensi kelas kuartil
l = panjang kelas / interval

panjang kelas : lihat salah satu kelas, misalnya kelas pertama 42 - 51 maka panjang kelasnya : (51 - 42) + 1 = 10

Q3, i=3 ----- 3/4 * 40 = 30
30 berada di kumulatif pada kelas 82 - 91 (lihat frekuensi kumulatif)

Qi = bi + ( (i/4 . N - F) / f ) . l
Q3 = 81.5 + ( (3/4 . 40 - 27) / 7 ) . 10
Q3 = 81.5 + ( 30 - 27) / 7 ) . 10

Q3 = 81.5 + 3/ 7 . 10

Q3 = 81.5 + 30/7

Q3 = 81.5 + 4.29

Q3 = 85.79

Jawaban : D

Soal Ujian Tingkat SMA / SMK Kelas 12 Matematika Wajib no 24

24. Diketahui lingkaran dengan persamaan (x - 3)^2 + (y - 4)^2 = 10. Titik pusat dan jari jari lingkaran tersebut berturut turut adalah ...

a. (3,4) dan √10

b. (- 3, 4) dan √10

c. (3, - 4) dan √10

d. (3 , 4) dan 10

e. (- 3, - 4) dan 10

Jawaban :

persamaan (x - 3)^2 + (y - 4)^2 = 10 memiliki bentuk persamaan lingkaran :

(x - a)^2 + (y - b)^2 = r^2

dengan pusat (a,b) dan jari jari r

maka,

titik pusat lingkaran tersebut adalah : (3, 4)

dan jari - jarinya = √10

Jawaban : A

Soal Ujian Tingkat SMA / SMK Kelas 12 Matematika Wajib no 23

 23. Kurva y = x^2 + 1 refleksikan terhadap garis x + y = 0. Bayangan kurva tersebut adalah ...

a. x^2 + y - 1 = 0

b. x^2 + y + 1 = 0

c. y^2 - x + 1 = 0

d. y^2 + x - 1 = 0

e. y^2 + x + 1 = 0

Jawaban :

Kurva y = x^2 + 1

refleksi terhadap garis 

x + y = 0

y = -x

maka,

x ' = - y

y = - x'

y ' = - x

x = - y'

sehingga kurvanya menjadi :

y = x^2 + 1

- x' = (-y')^2 + 1

- x' = y^2 + 1

0 = y^2 + x' + 1

y^2 + x + 1 = 0

Jawaban : E

Soal Ujian Tingkat SMA / SMK Kelas 12 Matematika Wajib no 22

22. Amad menyandarkan tangga ke dinding rumahnya untuk mengganti genteng yang bocor. Panjang tangga tersebut adalah 3m dan membentuk sudut sebesar 60° dengan tanah. Jarak dasar tangga dengan dinding adalah ...

a. 6m

b. 3√3 m

c. 3√2 m

d. √3 m

e. 1 1/2 m

Jawaban :

Jawaban : E

Soal Ujian Tingkat SMA / SMK Kelas 12 Matematika Wajib no 21

 21. Didefinisikan f(x) = 2 sin (x - 30°) + 2. Fungsi tersebut mempunyai nilai maksimum ...

a. 6

b. 5

c. 4

d. 3

e. 2

Jawaban :

f(x) = 2 sin (x - 30°) + 2

nilai maksimum dari sinus adalah 1, sehingga

f (x) = 2 . 1 + 2

f (x) = 2 + 2

f (x) = 4

Jawaban : C

Soal Ujian Tingkat SMA / SMK Kelas 12 Matematika Wajib no 20

 20. Terdapat segitiga sembarang ABC. Ruas garis AB = 6cm dan ruas garis AC = 8 cm. Jika ruas garis AB dan ruas garis AC membentuk sudut 120° maka panjang rusuk BC adalah ...

a. 3√37

b. 2√37

c. √37

d. 37

e. 148

Jawaban :

Jawaban : B

Soal Ujian Tingkat SMA / SMK Kelas 12 Matematika Wajib no 19

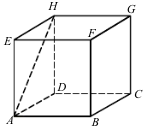
19. Diketahui kubus ABCD.EFGH dengan panjang rusuk 12 cm. Jarak dari titik C ke diagonal sisi AH adalah ...

a. 12√3 cm

b. 12√2 cm

c. 12 cm

d. 6√6 cm

e. 6√3 cm

Jawaban :

Soal Ujian Tingkat SMA / SMK Kelas 12 Matematika Wajib no 18

18. Balok ABCD.EFGH mempunyai ukuran panjang AB = 8cm, lebar AD = 6cm, dan tinggi AE = 5cm. Nilai tangen sudut yang dibentuk oleh ruas garis AD dan ruas garis BF
adalah ...

a. 5/6

b. 3/5

c. 1/2

d. 1

e. 2

Jawaban :

Soal Ujian Tingkat SMA / SMK Kelas 12 Matematika Wajib no 17

17. Luas daerah yang dibatasi oleh kurva f(x) = (x - 1)^2 + 1, sumbu-x, sumbu-y, dan garis x - 2 = 0 adalah ...

a. 2/11

b. 3/11

c. 3/8

d. 8/3

e. 11/3

Jawaban :

Jawaban : D

Soal Ujian Tingkat SMA / SMK Kelas 12 Matematika Wajib no 16

16. Pak Eko ingin membuat kandang berbentuk persegi panjang untuk ayam peliharaannya seluas 324m^2. Kandang tersebut akan dipagari dengan kawat duri seharga Rp 12.000,- per meter. Pernyataan berikut yang benar adalah ...

a. Jika lebar kandang 9 meter, biaya pemasangan kawat akan minimum

b. Jika lebar kandang 22 meter, biaya pemasangan kawat akan minimum

c. Jika panjang kandang 36 meter, biaya pemasangan kawat akan minimum

d. Biaya pemasangan kawat minimum adalah Rp 864.000,- 

e. Biaya pemasangan kawat minimum adalah Rp 432.000,-

Jawaban :

luas persegi panjang = p . l

pak eko ingin membuat kandang dengan luas 324m^2, sehingga

L = 324

p . l = 324

l = 324/p

perhitungan pagar untuk kandang menggunakan rumus keliling persegi panjang :

Keliling = 2 (p + l)

Keliling = 2 (p + 324/p)

Keliling = 2p + 648/p

f(p) = 2p + 648/p

untuk mendapatkan titik optimum, maka turunan pertama dari fungsi = 0

f ' (p) = 2 + (- 1) 648/p^2

0 = 2 - 648/p^2

648/p^2 = 2

648 = 2p^2

p^2 = 324

p = 18 (nilai positif karena panjang atau lebar tidak mungkin bernilai negatif)

hitung nilai l

l = 324 / p

l = 324 / 18

l = 18

maka kelilingnya menjadi :

Keliling = 2 (18 + 18)

Keliling = 2 (36)

Keliling = 72

Biayanya menjadi = 72 . 12rb = 864.000

(D)

Soal Ujian Tingkat SMA / SMK Kelas 12 Matematika Wajib no 15

15. Grafik fungsi f(x) = 4x^3 - 18x^2 - 48x - 1 naik pada interval ...

a. - 1 < x < 4

b. - 4 < x < 1

c. x < - 1 atau x > 4

d. x < - 4 atau x > 1

e. x < - 4 atau x > - 1

Jawaban :

fungsi akan naik apabila f '(x) > 0

maka, hitung dulu turunan pertama dari f(x) = f ' (x) 

f(x) = 4x^3 - 18x^2 - 48x - 1

f ' (x) = 12x^2 - 36x - 48

f ' (x) > 0

12x^2 - 36x - 48 > 0

x^2 - 3x - 4 > 0

(x - 4) (x + 1) > 0

titik pembuat 0 nya :

x = 4 atau x = - 1

bila x = 0, maka (x - 4) (x + 1) bernilai negatif

bila x = 5, maka (x - 4) (x + 1) bernilai positif

bila x = - 2 maka (x - 4) (x + 1) bernilai positif

karena yang dicari adalah f ' (x) > 0 atau bernilai positif, maka interval grafik naik :

x < - 1 atau x > 4

(C)

Soal Ujian Tingkat SMA / SMK Kelas 12 Matematika Wajib no 14

14. Hasil ∫ 2x^2 √(4x^3 - 5) dx adalah ...

a. 1/3 (4x^3 - 5) √(4x^3 - 5) + c

b. 1/6 (4x^3 - 5) √(4x^3 - 5) + c

c. 1/9 (4x^3 - 5) √(4x^3 - 5) + c

d. 1/12 (4x^3 - 5) √(4x^3 - 5) + c

e. 1/18 (4x^3 - 5) √(4x^3 - 5) + c

Jawaban :

∫ 2x^2 √(4x^3 - 5) dx

= 2 ∫ x^2 √(4x^3 - 5) dx

misalkan

u = 4x^3 - 5

du = 12x^2 dx

1/12 du = x^2 dx

lanjutkan dengan subtitusi x^2 dx dengan 1/12 du

= 2 ∫ x^2 √(4x^3 - 5) dx

= 2 ∫ 1/12 √u du

= 2 . 1/12 ∫ √u du

= 1/6 ∫ √u du

= 1/6 . ∫ (u)^1/2 du

= 1/6 . 2/3 . u^3/2

= 1/9 . u^3/2

= 1/9 (4x^3 - 5)^3/2 + c

= 1/9 (4x^3 - 5) √(4x^3 - 5) + c

(C)

Soal Ujian Tingkat SMA / SMK Kelas 12 Matematika Wajib no 13

13. Nilai dari lim x → ∞

(√(x^2 + 3x) - x + 1)) adalah 

a. 1/2

b. 3/2

c. 5/2

d. 2/3

e. 2/5

Jawaban :

untuk limit tak terhingga, 

buat ke dalam bentuk :
lim x→∞ (√(x^2 + 3x) - √(x + 1)^2)

lim x→∞ (√(x^2 + 3x) - √(x² + 2x + 1))

a = 1
b = 3

p = 1
q = 2

karena a = p makan nilai limit = L
L = (b - q) / 2√a
L = (3 - 2) /2√1
L = 1/2

(A)

Soal Ujian Tingkat SMA / SMK Kelas 12 Matematika Wajib no 12

12. Nilai dari lim x → 1 

(x^2 - 3x + 2) / (x^2 - 4x + 3) adalah ...

a. 0.25

b. 0.33

c. 0.67

d. 0.50

e. 0.75

Jawaban :

lim x → 1 

(x^2 - 3x + 2) / (x^2 - 4x + 3)

= 

lim x → 1 

(x - 2)(x - 1)/ (x - 3)(x - 1)

= 

lim x → 1 

(x - 2)/ (x - 3)

= (1 - 2) / (1 - 3)

=  - 1/ -2

= 1/2

= 0.5

(D)

Soal Ujian Tingkat SMA / SMK Kelas 12 Matematika Wajib no 11

11. Diketahui persamaan x^2 + (p - 3) x + 9 = 0. Jika persamaan tersebut memiliki akar-akar kembar, maka nilai p yang memenuhi syarat adalah ...

a. p = 3 atau p = - 3

b. p = 3 atau p = 6

c. p = - 3 atau p = - 9

d. p = - 3 atau p = 9

e. p = 6 atau p = 9

Jawaban :

syarat persamaan yang memiliki akar persamaan kembar ialah D = 0 (determinan = 0)

x^2 + (p - 3) x + 9 = 0

a = 1

b = p - 3

c = 9

D = 0

b^2 - 4ac = 0

(p - 3)^2 - 4 (1) (9) = 0

p^2 - 6p + 9 - 36 = 0

p^2 - 6p - 27 = 0

(p - 9) (p + 3) = 0

p = 9 atau p = - 3

(D)

Soal Ujian Tingkat SMA / SMK Kelas 12 Matematika Wajib no 10

10. Sherin, Doni, dan Harry pergi ke suatu toko buku untuk membeli buku, pensil, dan pena. Sherin membeli 5 buku, 2 pensil, 3 pena seharga Rp 50.000,- . Doni membeli 4 buku, 3 pensil, dan 2 pena seharga Rp 42.500,- dan Harry membeli 3 buku, 1 pensil, dan 2 pena seharga Rp 30.500,- . Jika Budi membeli 4 buku, 2 pensil, dan 2 pena di toko yang sama, Budi harus membayar sebesar ...

a. Rp 52.000,-

b. Rp 45.000,-

c. Rp 42.000,-

d. Rp 40.000,-

e. Rp 39.000,-

Jawaban :

misalkan :

buku = x

pensil = y

pena = z

maka,

untuk sherin :

    5x + 2y + 3z = 50.000 ... (i)

untuk doni :

    4x + 3y + 2z = 42.500 ... (ii)

untuk harry :

    3x + y + 2z = 30.500 ... (iii)

gunakan metode eliminasi dan substitusi untuk mencari nilai x, y , dan z

eliminasi (i) (dan (ii) dengan (i) x 2 dan (ii) x 3, agar z nya habis

10x + 4y + 6z = 100.000

12x + 9y + 6z = 127.500

------------------------------------ -

- 2x - 5y = - 27.500

2x + 5y = 27.500 ... (iv)

eliminasi (i) dan (iii) dengan (i) x 2 dan (iii) x 3, agar z nya habis

10x + 4y + 6z = 100.000

9x + 3y + 6z = 91.500

------------------------------------ -

x + y = 8.500 

x = 8.500 - y ... (v)

substitusi nilai x ke dalam persaman (iv)

2x + 5y = 27.500

2(8500 - y) + 5y = 27.500

17.000 - 2y + 5y = 27.500

3y = 27.500 - 17.000

3y = 10.500

y = 3.500

masukkan nilai y ke dalam persamaan (v)

x = 8.500 - y

x = 8.500 - 3.500

x = 5.000

masukkan nilai x dan y ke salah satu persamaan antara (i) , (ii) dan (iii)

kita coba masukkan ke dalam persamaan (i)

5x + 2y + 3z = 50.000

5(5000) + 2(3500) + 3z = 50.000

25.000 + 7.000 + 3z = 50.000

32.000 + 3z = 50.000

3z = 50.000 - 32.000

3z = 18.000

z = 6.000

maka jika Budi membeli 4 buku, 2 pensil, dan 2 pena, harganya menjadi :

4x + 2y + 2z

= 4(5000) + 2(3500) + 2(6000)

= 20.000 + 7.000 + 12.000

= 27.000 + 12.000

= 39.000

(E)

Soal Ujian Tingkat SMA / SMK Kelas 12 Matematika Wajib no 9

9. Sebuah bola dijatuhkan dari ketinggian 10 meter di atas lantai sehingga bola memantul kembali dengan pantulan pertamanya mencapai 6 meter. Jika setiap pantulan mempunyai rasio yang sama, maka panjang lintasan bola hingga berhenti adalah ...

a. 30 meter

b. 35 meter

c. 40 meter

d. 50 meter

e. 100 meter

Jawaban :

diketahui :

ketinggian awal : H = 10 meter

pantulan pertama : U1 = 6 meter

rasio pantulan selalu sama, maka pantulan ini termasuk deret geometri tak hingga, maka

6 = 10 . r

r = 6/10

r = 3/5

Untuk menghitung panjang lintasan, lihat gambar di atas, untuk pantulan terjadi 2x ditambah dengan ketinggian awal 10meter. Oleh karena itu perhitungan lintasan akan dilakukan dengan U1 = 6 meter yang merupakan deret tak hingga lalu ditambahkan dengan 10meter sebagai ketinggian awal.

S∞ = a / (1 - r)

S∞ = 6 / (1 -3/5)

S∞ = 6 / (2/5)

S∞ = 6 . 5/2

S∞ = 15

Panjang lintasan nya akan menjadi :

S = 10m + 2 . S∞

S = 10m + 2 .15m

S = 10 + 30 m

S = 40 meter (C)

Soal Ujian Tingkat SMA / SMK Kelas 12 Matematika Wajib no 8

8. Suatu deret geometri diketahui suku kedua bernilai -6 dan suku kelima bernilai 48. Suku kedelapan bernilai ...

a. - 384

b. - 192

c. - 64

d. 384

e. 192

Jawaban :

diketahui :

deret geometri

U2 = - 6

U5 = 58

yang ditanya : U8 ?

Un = a . r ^ (n -1)

U2 = a . r ^ (2 - 1)

- 6 = a . r

U5 = a . r ^ (5 - 1)

48 = a . r ^ (4)

48 = a . r . r^3

48 = - 6 . r^3

48 / - 6 = r^3

- 8 = r^3

r = - 2

maka nilai a :

- 6 = a . r

- 6 = a . (- 2)

3 = a

a = 3

suku ke delapan dari deret geometri tersebut :

U8 = a . r ^ (8 - 1)

U8 = 3 . (-2) ^ 7

U8 = 3 . - 128

U8 = - 384 (A)

Soal Ujian Tingkat SMA / SMK Kelas 12 Matematika Wajib no 7

7. Ada suatu tuntunan dari Rasulallah yang secara singkat dapat dinyatakan dalam dua kalimat, yaitu :

1) Kejujuran akan membawamu pada kebaikan

2) Kebaikan akan menghantarkanmu ke surga Allah SWT

Abdullah sangat meyakini itu dan senantiasa berlaku jujur dalam setiap urusan, maka dapat disimpulkan bahwa ...

a. Abdullah jujur dan akan masuk surga Allah SWT

b. Abdullah akan masuk surga Allah SWT

c. Abdullah tidak jujur maka tidak akan masuk surga Allah SWT

d. Abdullah jujur jika dan hanya jika akan masuk surga Allah SWT

e. Abdullah jujur atau akan masuk surga Allah SWT

Jawaban :

premis 1 : Kejujuran akan membawamu pada kebaikan

p : kejujuran

q : kebaikan

p → q

premis 2 : Kebaikan akan menghantarkanmu ke surga Allah SWT

q : kebaikan

r : surga Allah SWT

q → r

premis 1 : p → q

premis 2 : q → r

konklusi : p → r

premis 3 : Abdullah jujur di setiap urusan (p)

maka kesimpulannya : r

Abdullah akan masuk surga Allah SWT (B)